중3 과학 별의 등급 문제 및 풀이
중학교 3학년 학생들의 기말고사는 빠르죠?? 빠른 학교는 다음 주부터 시작하는 것 같네요. 제가 과외하는 녀석들이 다음 주부터 시험이라서~~~
오늘도 별의 등급에 관한 문제입니다. 어제 네이버 지식인에 올라온 문제이지만, 아직도 별의 등급을 어려워하는 친구들이 많은 것 같아서, 다시 한번 문제를 풀어보도록 할게요^^
- 문제풀이-
우선, 별의 등급은 별의 밝기를 나타내는 수입니다. 근데, 등급이 크면 어두운 별이고, 등급이 작으면 밝은 별입니다. 이 정도는 알고 있죠?? 그리고 밝기는 거리의 제곱에 반비례합니다. 즉, 거리가 멀어지면 밝을까요?? 어두울까요??? 예를 들면 여러분 앞에 핸드폰이 있죠?? 핸드폰을 손으로 잡고 볼 때와 핸드폰을 1미터 떨어진 곳에 있을 때 밝기를 비교하면 어디에 있을 때 더 밝을까요?? 어렵지 않죠?? 가까이에 있을 때 더 밝아요. 따라서 멀어지면 멀어질수록 어둡다는 것 알 수 있습니다. 그럼, 별도 마찬가지예요. 지금 있는 거리에서 더 멀어지면 더 어둡게 보이겠죠?? 그리고 등급은 커질 것이고요~~ 이해가 되시죠??
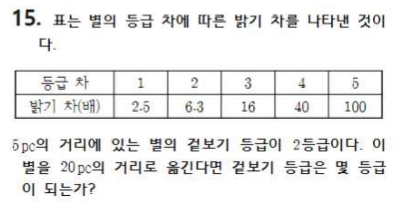
두 번째, A라는 별의 등급이 1등급이고, B라는 별이 2등급이라면 A별이 등급이 작으므로 밝은 별이죠?? 그럼 A별은 B별보다 얼마나 밝을까요??? 이때 밝기차는 등급차로 계산을 합니다. A별이 1등급이고, B별은 2등급이므로, 두 별의 등급차는 1등급 차이죠. 그럼 밝기는 2.5배 차이가 나요. 두 별의 등급차가 2등급 차이면 2.5의 제곱으로 약 6.3배, 3등급 차이면 2.5의 세제곱으로 약 16배, 4등급 차이면 2.5의 네제곱으로 약 40배, 5등급 차는 2.5의 다섯 제곱으로 약 100배 밝기차가 생깁니다.
세 번째, 문제를 보면 5pc(파섹으로 읽어서 그냥 파섹으로 적을게요)의 거리에 있는 별을 20파섹으로 가져가면 지금보다 거리가 4배 멀어진 것이죠? 그럼 거리가 4배 멀어지면 밝기는 16배 어두워집니다.(여기까지는 첫 번째 부분이죠.) 16배는 표에서 2.5의 세제곱배이므로, 3등급 차가 됩니다. (여기는 두 번째 부분이죠.) 5파섹에 있을 때 별의 등급이 2등급인데, 거리가 4배 멀어지면 밝기는 16배 어두워지고, 16배는 2.5의 세제곱배이므로, 3등급 차이죠. 어두운 별이므로 등급은 커져야 하므로, 현재 등급의 3등급을 더하면 20파섹에 있을 때 등급이 됩니다. 따라서 2등급 + 3등급이므로, 5등급이 되는 것이죠.
이해가 되시나요???
만약, 거리가 가까워지면 밝기는 밝아지겠죠??? 그러면 등급을 구할 때는 현재의 등급에서 해주면 됩니다.
이해가 안 되면 천천히 읽어보시고, 문제를 푸는 것도 좋지만, 내용을 알고 푸는 것이 훨씬 큰 도움이 된다는 것.. 꼭 기억하세요~~